math_tools.cpp File Reference

#include "math_tools.h"
#include <stdexcept>
#include <cmath>
#include <cstdint>

Include dependency graph for src/math_tools.cpp:

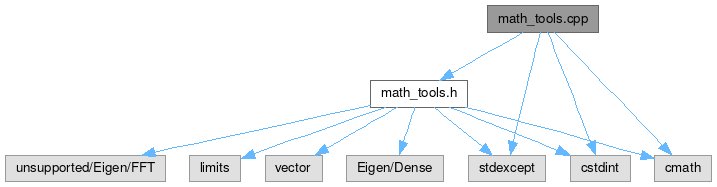
Go to the source code of this file.

Functions
Eigen::MatrixXd	math_tools::box_muller (const Eigen::VectorXd &vRand)
std::pair< Eigen::VectorXd, Eigen::VectorXd >	math_tools::compute_spectrum (Eigen::VectorXd &data, int N)
Eigen::MatrixXd	math_tools::generate_normal_random_matrix (const size_t n, const size_t m)
Eigen::MatrixXd	math_tools::generate_uniform_random_matrix_0_1 (const size_t n, const size_t m)
Eigen::VectorXd	math_tools::hamming_window (int N)
Eigen::MatrixXd	math_tools::squareDistance (const Eigen::MatrixXd &a)
Eigen::MatrixXd	math_tools::squareDistance (const Eigen::MatrixXd &a, const Eigen::MatrixXd &b)
double	math_tools::stdandard_deviation (Eigen::VectorXd &input)

Detailed Description

Provides mathematical tools needed for the Gaussian process toolbox.

Date

2014-2017

Copyright

Max Planck Society

Author

Edgar D. Klenske edgar.nosp@m..kle.nosp@m.nske@.nosp@m.tueb.nosp@m.ingen.nosp@m..mpg.nosp@m..de

Stephan Wenninger steph.nosp@m.an.w.nosp@m.ennin.nosp@m.ger@.nosp@m.tuebi.nosp@m.ngen.nosp@m..mpg..nosp@m.de

Raffi Enficiaud raffi.nosp@m..enf.nosp@m.iciau.nosp@m.d@tu.nosp@m.ebing.nosp@m.en.m.nosp@m.pg.de

Definition in file src/math_tools.cpp.

Function Documentation

box_muller()

Eigen::MatrixXd math_tools::box_muller

(

const Eigen::VectorXd &

vRand

)

Apply the Box-Muller transform, which transforms uniform random samples to Gaussian distributed random samples.

Definition at line 109 of file src/math_tools.cpp.

compute_spectrum()

std::pair< Eigen::VectorXd, Eigen::VectorXd > math_tools::compute_spectrum	(	Eigen::VectorXd &	data,
		int	N = 0 )

Calculates the spectrum of a data vector.

Does pre-and postprocessing:

• The data is zero-padded until the desired resolution is reached.
• ditfft2 is called to compute the FFT.
• The frequencies from the padding are removed.
• The constant coefficient is removed.
• A list of frequencies is generated.

Definition at line 151 of file src/math_tools.cpp.

generate_normal_random_matrix()

Eigen::MatrixXd math_tools::generate_normal_random_matrix	(	const size_t	n,
		const size_t	m )

Generates normal random samples. First it gets some uniform random samples and then uses the Box-Muller transform to get normal samples out of it

Definition at line 138 of file src/math_tools.cpp.

generate_uniform_random_matrix_0_1()

Eigen::MatrixXd math_tools::generate_uniform_random_matrix_0_1	(	const size_t	n,
		const size_t	m )

Generates a uniformly distributed random matrix of values between 0 and 1.

Definition at line 95 of file src/math_tools.cpp.

hamming_window()

Eigen::VectorXd math_tools::hamming_window

(

int

N

)

Computes a Hamming window (used to reduce spectral leakage of subsequent DFT).

Definition at line 187 of file src/math_tools.cpp.

squareDistance() [1/2]

Eigen::MatrixXd math_tools::squareDistance

(

const Eigen::MatrixXd &

a

)

Single-input version of squaredDistance. For single inputs, it is assumed that the pairwise distance matrix should be computed between the passed vector itself.

Definition at line 90 of file src/math_tools.cpp.

squareDistance() [2/2]

Eigen::MatrixXd math_tools::squareDistance	(	const Eigen::MatrixXd &	a,
		const Eigen::MatrixXd &	b )

The squareDistance is the pairwise distance between all points of the passed vectors. I.e. it generates a symmetric matrix when two vectors are passed.

The first dimension (rows) is the dimensionality of the input space, the second dimension (columns) is the number of datapoints. The number of rows must be identical.

Parameters

a	a Matrix of size Dxn
b	a Matrix of size Dxm

Returns

a Matrix of size nxm containing all pairwise squared distances

Definition at line 28 of file src/math_tools.cpp.

stdandard_deviation()

double math_tools::stdandard_deviation

(

Eigen::VectorXd &

input

)

Computes the standard deviation of a vector... which is not part of Eigen.

Definition at line 198 of file src/math_tools.cpp.